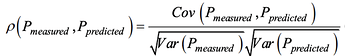I was following the course “Lab 2_2 - CPA on Hardware AES Implementation”, yet I dont understand the steps used there. I understand that in hardware, AES Round can be performed with just one cycle, so we arent able to use the old method for software implementations where we can compare the different hamming weights correlation in power. I read that we compare the hamming distance, but I cant follow up on the steps there. Could you explain me how the attack works? Could this attack be also repeated on AES Hardware Accelerators used in e.g. HSMs?
The Hamming distance leakage model works between two consecutive states.
The state here is a set of registers of sequential logic which is stores intermediate states and which can change its value only on coming new clock pulse.
Convenient point to apply HD leakage model for AES-128 is the final AES output (10-th round) and 9-th round.
To apply the attack, we first guess the AES key byte in the range [0 … 256] to guess the output of 9-th round and using known cipher output:
![]()
then we calculate the predicted power using HD model. The Hamming distance of two S1 and S2 states HD(S1, S2) is HW(S1 xor S2).
Ultimately we calculate the Pearson correlation coefficient using
Pearson correlation measures linearity between Pmeasured (collected traces) and Ppredicted (HD).
If correlation has the values close to -1 and 1, there is a strong correlation and more likely we guess the correct key byte. If correlation is close to 0, guess the incorrect key byte.
These steps are repeated 16 times for each key byte.
Regarding an attack against HSM. It depends of HSM implementation.
Most of HSM’s have countermeasures against SCA and you cannot attack its AES implementation described in the Lab 2.2.
The possible countermeasures are noise in the power line, drift of internal clock, masking of AES HW implementation.
Arent we guessing the key of the 10th round? In your case, what are the states S1 and S2?
Why cant we use Hamming Weight here?
Where do we actually measure the power?
I understood it as following:
We are trying to guess K10 (last roundkey), we know the last ciphertext C10.
Looking at your example, D10 is just C9 xor K9, or going backwards its as you stated in your equation.
But when the plaintext is being encrypted, we cannot go backwards to measure it the way you did, right?
I understand that we need to gather the power at D10. But I dont understand how we can correlate that to
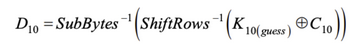
as we cannot decrypt the message. Are the power traces the same for C9xorK9 as they are for this case? I still dont understand the use of hamming distance here…
Yes, we guess the key used by the 10-th round. AES-128 schedules 11 round keys. So, we guess 11-th key. After doing reverse scheduling, you can get the first key which actually is the AES key itself.
It is just for generic explanation. S1 and S2 don’t relate with the first and second AES rounds.
Everywhere. But we need exactly the place where leakage happens. For AES-128 HW implementation this place is output of the 9-th round stored in the registers.
Suppose, your victim CPU is clocked by exactly the same clock source as CW ADC and the victim CPU has 1 clock per AES round performance. In this case leakage will happen ONLY at one single sample captured by the ADC.
It is very important that the clock passed to the ADC would be equal or greater than the clock passed to the CW ADC. Otherwise, you have all chances to miss the leakage point and not be able to guess the key.
Actually, Hamming Distance (HD) goes through Hamming Weight (HW).
The logic is in the below code:
def lastround_HD_gen(byte):
# selection_with_guess function must take 2 arguments: value and guess
def selection_with_guess(value, guess):
INVSHIFT_undo = [0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 12, 1, 6, 11]
st10 = value[INVSHIFT_undo[byte]]
st9 = inv_sbox[value[byte] ^ guess]
return hamming(st9 ^ st10)
return selection_with_guess
def hamming(value):
r = np.uint32(0)
while value:
r += _hw[value & 0xFF]
value >>= 8
return r
Not exactly. D10 is the input of the 10-th round and hence, it is output of the 9-th round.
So, we can say that the D10 is C9. Also pay attention that AES-128 has 11 round keys for 10 AES rounds.
We cannot decrypt but we can guess and measure correlation!
I still dont understand the point where everything takes just one clock cycle. There is a lot happening, like all the operations. Is the power trace still similar to the software implementation, but it all happens faster? What I mean is, for the software implementation I simply recorded at the start of the round1, where SubBytes is performed. When I would record the whole power trace of round1, is it the same power trace I would get when recording the hardware implementation (whole round), just in one cycle than split between many cycles? Or does the power trace look different and I need way more traces to find any correlation (because a lot of more operations are executed in the 1 cycle).
Another question is, what if I cant sample synchronously? Do I just need to increase the sampling rate so that I wont miss that point?
Are we actually attacking round9 or round10 here? From my understanding, to get the D10, also C9, we need to record the round 9 and then perform the mathematical comparison(correlation) with inversed round10?
Let me ask a question before…
Do you familiar with Verilog HDL language and whether you have general understanding of how hardware works?
Yes, I got some basic understanding. I just dont know how to imagine such leakage when everything happens in one clock cycle. How or where am I supposed to measure the electromagnetic radiation? Is asynchronous sampling even possible in this case? Or is there a way to provide external clock to the oscilloscope?
I would recommend to read what is the sequential logic first. Then you will answer yourself all your questions.
All I read is that it is very hard to perform whole AES round in one clock cycle on the hardware. Does the CWnano actually support this?
Would it be possible for you to answer some of my previous questions, especially about the asynchronous sampling?
also what wonders me, why or how different is the leakage of a software implementation compared to hardware implementation? why is hardware harder to attack? is it just too fast and you may miss some information (what if you increase the sampling rate)? are the voltage fluctuations different less visible on hardware than the standard software implementation on a chip?
It is difficult to go further until you get strong understanding of what is sequential logic. Also, I would recommend to learn quickly basics of Verilog HDL.
You have to keep in mind you measure dynamic power consumption changes when the AES state is stored in the registers. This very simplifies the attack model. You don’t need to know what happens in the middle of clock ticks.
Without these knowledge it is difficult to find answers to the questions you asked.
I thought its not really stored in the registers, since its all wired and goes through hardware. So there are no steps where you “hold breath” and save things, it all goes in one cycle and you get a different state. If the calculation (and measurement) of the power is spread for more cycles (=more time) then it is easier to distinguish the SBOX operation from the MixColumns, if everything happens in one cycle and you can only record one cycle, you have to analyse the trace of a whole round and not just the picked SBOX operation, or am I wrong here?
In a real case scenario, how many traces do you need to gather to attack such hardware implementation? Also, sampling asynchronously, you need a really high sampling rate to capture that one cycle
“Registers” here are in terms of Verilog. Actually, it is flip-flops.
This is not true for the real implementations. There is a thing called propagation delay. It makes almost impossible to implement true combinational logic implementation of AES.
The best AES implementation (I saw) for ASIC was 3 rounds per cycle.
Here is HW AES implementation which NewAE guys use for their samples. You can see how the round output is stored in the register state.