Hello everyone,
There are some magical numbers to me in this demo.
1. One comes to the very first definition of the list, poi. Why -6 and 7? Further, how do we know the metric, get_sums, should subtract power while the index i is negative? What’s the physical significance of this metric?
2. The second part is in the section Correlation Attack, why are rupdate_cycles = 8? So are the rest numbers in the same cell.
Alan
Hi Alan,
1- From the notebook:
# these are the clock cycles for which we sum the power measurement
# for positive numbers, we add the power measurement at that clock cycle;
# for negative numbers, we substract the power measurement at abs(clock cycle).
poi = [4202, -6, 7]
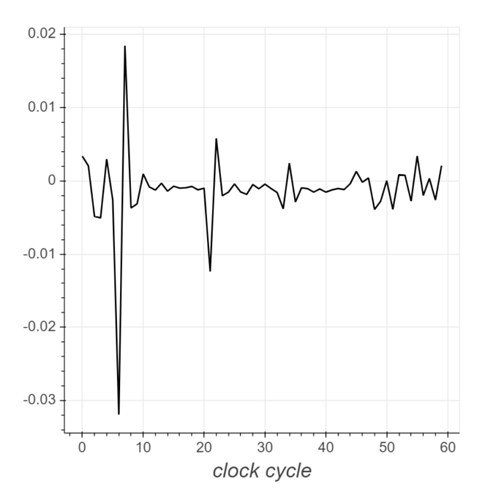
If you zoom on the difference of averages plot (just before “bingo!” in the notebook), you should see something like this:
We see a significant difference between the averages at cycles 6 and 7. Now if we were to add the two power measurements from cycle 6 and 7, they would almost cancel each other out, and this wouldn’t be very helpful towards picking out the difference between a k bit = 1 versus a k bit = 0.
We’re trying to build a metric that best distinguishes 1’s from 0’s. So the -6, 7 (and 4202) numbers aren’t magical – they are just what the difference of means plot reveal to be where a 1 differs from a 0. And that is the significance of this metric.
The cycle index’s sign is accounted for by def get_sums() here:
power = trace.wave[c+abs(i)]
if i < 0:
sum -= power
else:
sum += power
2- If you look in the next cell where corrx, corry and corrz are computed, you’ll find that the correlations are computed over trace segments of rupdate_cycles clock cycles. We set this to 8 because the x, y, z coordinates are each read or written over 8 clock cycles (256-bit numbers into a 32-bit wide memory). I’ll update the notebook to clarify this!
Jean-Pierre
1 Like
Hey, Jean
Sorry for such a late reply, many thanks for ur elaborate explanations.
I just found a slight difference in my situation,
in the following figure, my poi should be poi [4202, -6, 12], right?
It would appear so. What is your setup exactly? As mentioned in the notebook, the presented attack parameters were obtained for CW-Pro and CW305 100t FPGA.
Jean-Pierre
Mine: CW-Lite and CW305 100t FPGA.