Understanding the effect of shuffling on CPA correlation

Embedded Security Side Channel Power Analysis
1

Hi, I am trying to understand how shuffling the order of the S-Box lookup affects the number of traces needed for a successful attack. I am consulting ‘Power Analysis Attacks: Revealing the Secrets of Smart Cards’ By Stefan Mangard et al.

Eq. 8.8 (on Page 210) states that : If the power consumption of l clock cycles is independently distributed and if the variances of the power consumption in all cycles are equal, the sum of the power consumption leads to the following correlation coefficient for the correct key hypothesis.
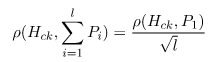
image

My question is: which operations are being ‘integrated’ for this to apply? So for the 16 S-Box lookups, if each lookup (i.e., L0, L1 …L15) can be in any of the 16 ‘positions’ per trace, does the attacker need to know where each of the lookups happens to do this integration?

Without this information, I’m not getting how integration can be done without a brute-force approach of checking every possible combination of positions.

Any help/clarity would be much appreciated!

2

I’m not familiar with that attack, but I would guess that you would indeed need to know where the lookups are happening. I’d imagine this can be done by some visual inspection of the power traces and some trial and error.

Alex

3

p. 210: By integration we mean that the attacker sums up the power consumption of l clock cycles.

So let’s take the example with 16 S-boxes and let’s assume for simplicity you have one clock cycle per S-box and you the processing order is shuffled. Then you would sum up the power consumption of these 16 clock cycles and proceed with the attack on these post-processed traces.